Tag: paper

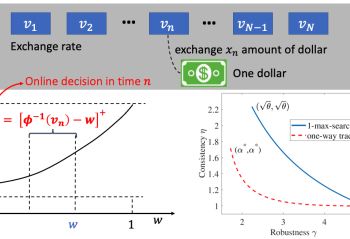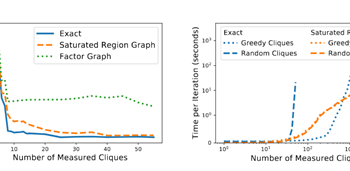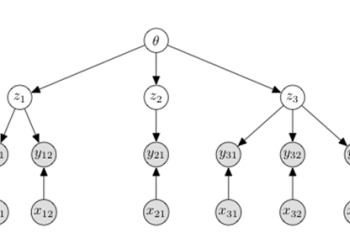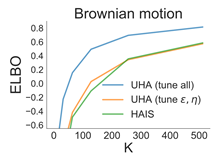
This paper studies a cooperative multi-armed bandit problem with M agents cooperating together to solve the same instance of a K-armed stochastic bandit problem. The agents are heterogeneous in their limited access to a local subset of arms; and their decision-making rounds. The goal is to find the global optimal arm and agents are able … Continue reading "Paper: Cooperative Stochastic Bandits with Asynchronous Agents and Constrained Feedback"

In this work, we leverage machine-learned predictions to design competitive algorithms for online conversion problems with the goal of improving the competitive ratio when predictions are accurate (i.e., consistency), while also guaranteeing a worst-case competitive ratio regardless of the prediction quality (i.e., robustness). We unify the algorithmic design of both integral and fractional conversion problems, … Continue reading "Paper: Pareto-Optimal Learning-Augmented Algorithms for Online Conversion Problems"

Differentially private algorithms for answering database queries often involve reconstruction of a discrete distribution from noisy measurements. PRIVATE-PGM is a recent exact inference based technique that scales well for sparse measurements and provides consistent and accurate answers. However it fails to run in high dimensions with dense measurements. This work overcomes the scalability limitation of … Continue reading "Paper: Relaxed Marginal Consistency for Differentially Private Query Answering"

It is difficult to use subsampling with variational inference in hierarchical models since the number of local latent variables scales with the dataset. Thus, inference in hierarchical models remains a challenge at large scale. It is helpful to use a variational family with structure matching the posterior, but optimization is still slow due to the … Continue reading "Paper: Amortized Variational Inference for Simple Hierarchical Models"

When faced with sequential decision-making problems, it is often useful to be able to predict what would happen if decisions were made using a new policy. Those predictions must often be based on data collected under some previously used decision-making rule. Many previous methods enable such off-policy (or counterfactual) estimation of the expected value of … Continue reading "Paper: Universal Off-Policy Evaluation"

When faced with sequential decision-making problems, it is often useful to be able to predict what would Annealed Importance Sampling (AIS) with Hamiltonian MCMC can be used to get tight lower bounds on a distribution’s (log) normalization constant. Its main drawback is that it uses non-differentiable transition kernels, which makes tuning its many parameters hard. … Continue reading "Paper: MCMC Variational Inference via Uncorrected Hamiltonian Annealing"

Consider an n x n Gaussian kernel matrix corresponding to n input points in d dimensions. We show that one In this work, we revisit REINFORCE and investigate if we can leverage other reinforcement learning approaches to improve learning. We formalize training a neural network as a finite-horizon reinforcement learning problem and discuss how this … Continue reading "Paper: Structural Credit Assignment in Neural Networks using Reinforcement Learning"