Paper: Pareto-Optimal Learning-Augmented Algorithms for Online Conversion Problems
By
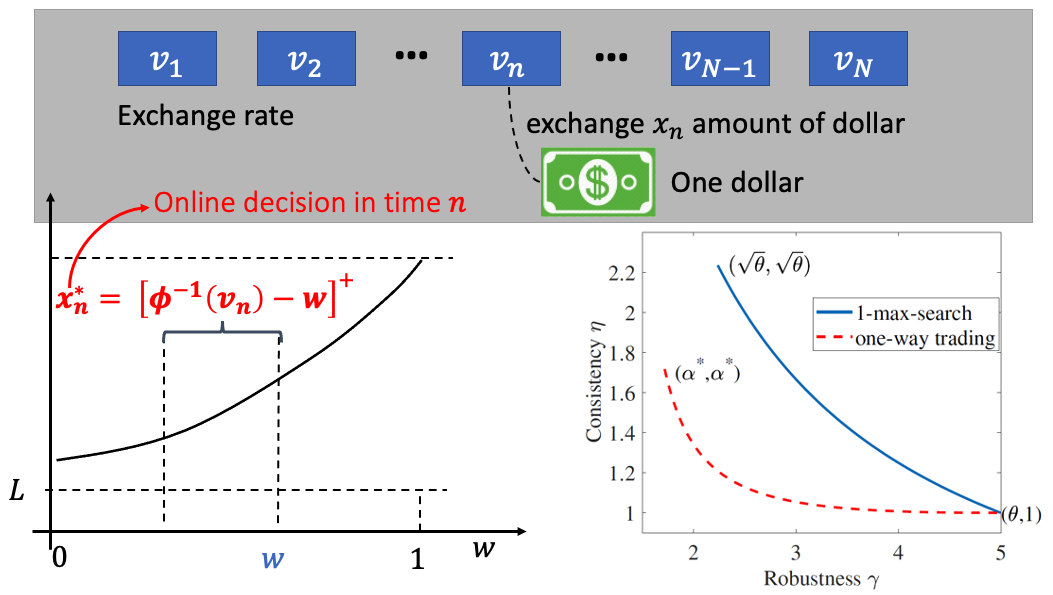
In this work, we leverage machine-learned predictions to design competitive algorithms for online conversion problems with the goal of improving the competitive ratio when predictions are accurate (i.e., consistency), while also guaranteeing a worst-case competitive ratio regardless of the prediction quality (i.e., robustness). We unify the algorithmic design of both integral and fractional conversion problems, into a class of online threshold-based algorithms (OTA). By incorporating predictions into the design of OTA, we achieve the Pareto-optimal trade-off of consistency and robustness, i.e., no online algorithm can achieve a better consistency guarantee given for a robustness guarantee. We demonstrate the performance of OTA using numerical experiments on Bitcoin conversion.Differentially private algorithms for answering database queries often involve reconstruction of a discrete distribution from noisy measurements. PRIVATE-PGM is a recent exact inference based technique that scales well for sparse measurements and provides consistent and accurate answers. However it fails to run in high dimensions with dense measurements. This work overcomes the scalability limitation of PRIVATE-PGM on dense data by relaxing consistency constraints. Our new approach works with many existing private query answering algorithms and improves scalability or accuracy with no privacy cost.
