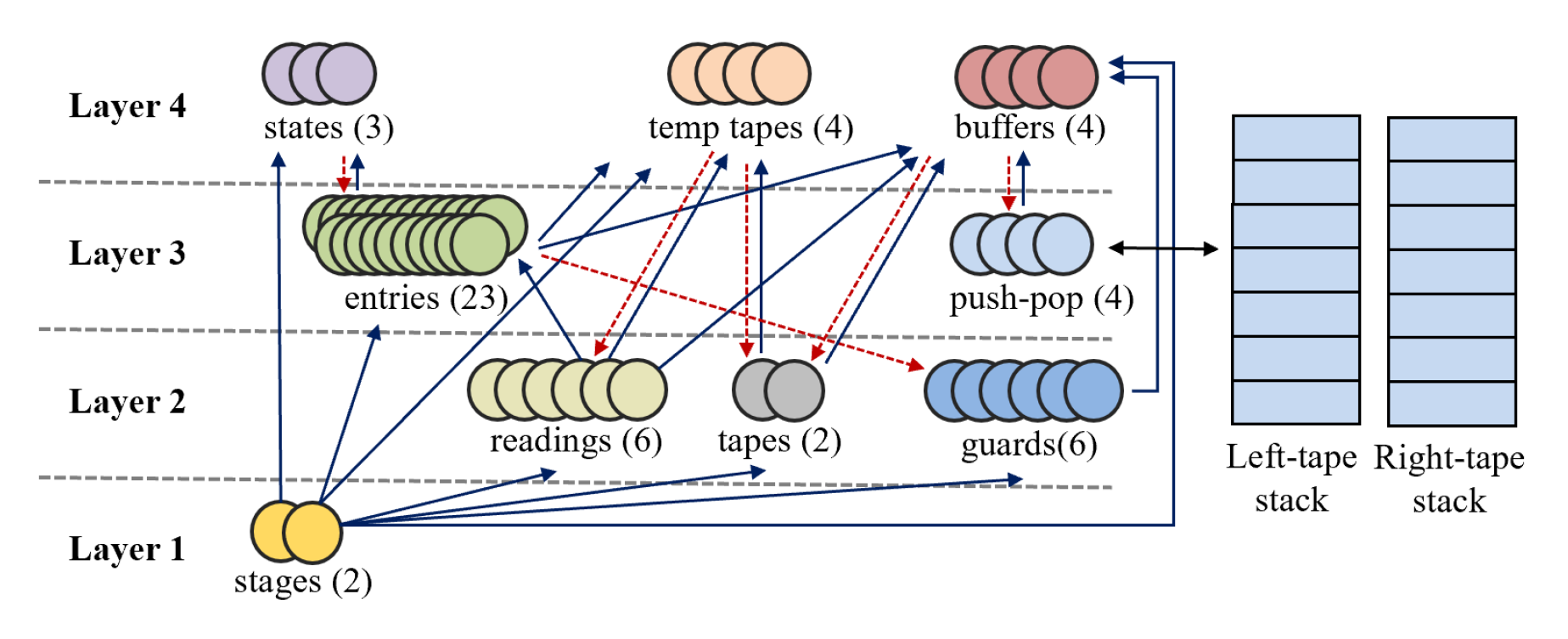
Previous works have proved that recurrent neural networks (RNNs) are Turing-complete. In the proofs, the RNNs allow for neurons with unbounded precision, which is neither practical in implementation nor biologically plausible. To remove this assumption, we propose a dynamically growing memory module made of neurons of fixed precision. We prove that a 54-neuron bounded-precision RNN with growing memory modules can simulate a Universal Turing Machine, with time complexity linear in the simulated machine’s time and independent of the memory size. The result is extendable to other stack-augmented RNNs. Furthermore, we analyze the Turing completeness of both unbounded-precision and bounded-precision RNNs.