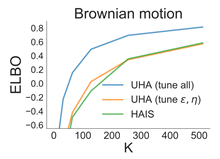
When faced with sequential decision-making problems, it is often useful to be able to predict what would Annealed Importance Sampling (AIS) with Hamiltonian MCMC can be used to get tight lower bounds on a distribution’s (log) normalization constant. Its main drawback is that it uses non-differentiable transition kernels, which makes tuning its many parameters hard. We propose a framework to use an AIS-like procedure with Uncorrected Hamiltonian MCMC, called Uncorrected Hamiltonian Annealing. Our method leads to tight and differentiable bounds. Additionally, we observe empirically that the ability to tune all of our method’s parameters using unbiased reparameterization gradients leads to significant gains in performance.