Benjamin Marlin

Offered: Spring 2022

Course Description: This seminar will introduce students to research in the area of Bayesian methods applied to deep neural network models. The course will begin with foundational readings on Markov chain Monte Carlo and variational Bayesian methods and proceed to cover recent advances that are enabling the application of Bayesian inference to increasingly large deep learning models. The course will also cover methods for accelerating prediction using Bayesian deep learning models and for evaluating Bayesian deep learning models. Students will need background in deep learning (such as provided by COMPSCI 682 or COMPSCI 689) and probabilistic graphical models (such as provided by COMPSCI 688). The seminar will focus on reading, presenting, and discussing classical and recent papers (1 credit) and a final project focusing on a Bayesian deep learning topic (3 credits). 1-3 credits.

• Location: LGRT 143.
• Time: Fridays 2:30-5:15pm
• Website: The course website will be hosted on Moodle.
• Course Syllabus

Required Background: Students will need background in deep learning (such as provided by COMPSCI 682 or COMPSCI 689) and probabilistic graphical models (such as provided by COMPSCI 688).

Computing: Access to a relatively modern computer will be required to complete a project for the course.

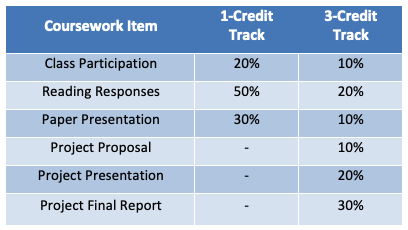
Coursework: The course includes two tracks. In the 1-credit track, coursework will consist of reading papers, writing paper responses, and presenting papers. The 3-credit track includes the completion of a substantial course project on Bayesian deep learning. The details are provided below including the weight of each course component and the grade thresholds for the course.

• 1-Credit Track: The course will cover one or two papers per week. Students will complete all readings and write a response for one research paper each week. Responses will be 250-500 words. Each student will participate in presenting one or two papers depending on final enrollment. Students will prepare an original presentations for the papers they present. All students are expected to participate in paper discussions.
• 3-Credit Track: Students will complete the work in the 1-credit track in addition to a substantial course project. The deliverables for the course project include a 2-page project proposal due by mid-semester, a final project presentation with demo (10-15 minutes), and a final project report in standard 8-page NeurIPS format (plus additional pages for references). Course projects will be completed individually.

Readings: The course will use readings from the primary literature with background provided by Machine Learning: A Probabilistic Perspective by Kevin Murphy. The Murphy text is available to UMass students for free through the UMass library. The initial topic list (subject to change based on enrollment and student interests in the class) is provided below.

• Week 1: Course Introduction. Review of classical MCMC methods.
• Week 2: Neal. Bayesian learning via stochastic dynamics. NeurIPS 1993.
• Week 3: Welling and The. Bayesian Learning via Stochastic Gradient Langevin Dynamics. ICML 2011.
• Week 4: Chen, Fox, and Guestrin. Stochastic Gradient Hamiltonian Monte Carlo. ICML 2014.
• Week 5: Zhang et al. Cyclical Stochastic Gradient MCMC for Bayesian Deep Learning. ICLR 2020.
• Week 6: Izmailov et al. Subspace Inference for Bayesian Deep Learning. UAI 2019.
• Week 7: Maddox et al. A Simple Baseline for Bayesian Uncertainty in Deep Learning. NeurIPS 2019.
• Week 8: Lakshminarayanan. Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles. NeurIPS 2017.
• Week 9: Review of classical variational inference methods and variational Bayes.
• Week 10: Blundell et al. Weight Uncertainty in Neural Networks. ICML 2015.
• Week 11: Gal and Ghahramani. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. ICML 2016.
• Week 12: Korattikara et al. Bayesian Dark Knowledge. NeurIPS 2015.
• Week 13: Final project presentations.